Draw a Box Lesson 3
Lesson 3: Polygons and Parameters
In the first lesson, nosotros taught the turtle how to draw a square. We ended up with a process that looks like this:
TO Foursquare REPEAT iv [ FORWARD 100 Correct ninety ] Cease
In this lesson, nosotros are going to meliorate upon this process. We are going to create a process that draws squares of any size. And we are going to create a procedure that draws other shapes.
Cartoon Squares of Whatsoever Size
Our SQUARE procedure is pretty skillful, but we can make it improve. Right now, the turtle only knows how to describe squares that are 100 pixels long on each side. Let's teach the turtle how to draw squares of whatever size.
We can practice this by using something called a "parameter". A parameter is like a fill-in-the-blank for a procedure. When you define a procedure, you go out some values bare. When you telephone call that process, you give it a value to utilise in that blank.
This may audio complicated, but it's non. In fact, you already know a procedure that takes a parameter: Forrad. When you give the turtle a "FORWARD" instruction, yous can't just say "FORWARD", you as well have to tell him how many screen dots to move forward. This number is a parameter.
We are going to make Square accept a parameter that tells the turtle how long each side should exist.
Activity: Press the "Edall" push and change the SQUARE function to the following:
TO Square :LENGTH Repeat iv [ Forward :LENGTH Correct 90 ] Finish
The ":LENGTH" is our parameter. When we use this Foursquare procedure, we have to put a number after it. The number we use volition be the number of pixels that the turtle moves frontward when drawing each side. For example, "SQUARE 10" tells the turtle to make a square with sides that are 10 pixels long.
Nosotros tin use our more powerful Foursquare procedure to draw an interesting design.
REPEAT 10 [ Square REPCOUNT * x ] |  |
Drawing a Polygon with any Number of Sides
Now the turtle tin draw a square of any size, but what about other shapes. What almost a triangle? What almost a polygon with five sides? What about a polygon with a hundred sides? Tin we make a single procedure that draws a polygon with whatsoever number of sides?
Permit's look at some lawmaking for drawing polygons and try to observe a design.
Exercise you see a pattern? All of these shapes were drawn by repeatedly moving forward and turning right. The number of times we echo equals the number of sides. The corporeality that we moved forward doesn't change. The amount we turn seems to get smaller with more sides.
Now for the hard part: how much should we turn? If you add upwardly the "exterior angles" of whatsoever airtight polygon, you always become 360°. In the shapes that we have fatigued, all angles are the same size. For example, in a triangle, we have iii angles. Since nosotros take to turn a total of 360° for all iii angles put together, each angle should be 360° divided by 3, or 120°.
So let'due south create a process that tin can draw all of the shapes to a higher place. We'll telephone call this procedure "POLYGON". By the manner, in Logo you split past using the "/" operator.
TO POLYGON :SIDES Repeat :SIDES [ FORWARD 100 RIGHT 360 / :SIDES ] END
Activity: Type in the POLYGON procedure and play around with it. What happens when you give it a number less than 3? What happens when you give it a large number, like 50?
Activity: Change the POLYGON procedure to have a :LENGTH parameter, similar we did for the Foursquare routine.
Activity: Create your own procedures that take a parameter. Y'all tin get-go from scratch or you lot can start with one of the samples from any lesson.
Sample Programs
TO RIGHTTRIANGLE :LENGTH Forrad :LENGTH Right 135 FORWARD :LENGTH * SQRT 2 RIGHT 135 FORWARD :LENGTH RIGHT 90 END TO PYRAMID Right 45 REPEAT iv [ REPEAT x [ RIGHTTRIANGLE REPCOUNT * x ] RIGHT 90 ] LEFT 45 Finish PYRAMID | 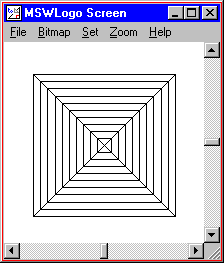 |
TO POLYGON :SIDES :LENGTH REPEAT :SIDES [ FORWARD :LENGTH Correct 360 / :SIDES ] END TO HEXAGONFLOWER :PETALS Echo :PETALS [ POLYGON 5 50 Right 360 / :PETALS ] Cease HEXAGONFLOWER x | 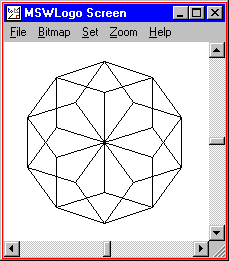 |
TO DOWNSLANT :LENGTH Echo 2 [ FORWARD :LENGTH Correct 135 Forrad 20 Correct 45 ] Right 135 Frontward 20 LEFT 135 Terminate TO UPSLANT :LENGTH REPEAT two [ FORWARD :LENGTH RIGHT 45 FORWARD twenty Right 135 ] Correct 45 FORWARD 20 LEFT 45 Terminate TO Sail REPEAT 2 [ DOWNSLANT 100 ] Echo 2 [ UPSLANT 100 ] DOWNSLANT 100 REPEAT 2 [ UPSLANT 50 ] DOWNSLANT 50 REPEAT ii [ DOWNSLANT ten ] UPSLANT 10 END SHEET | 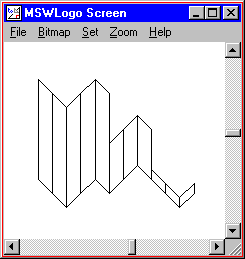 |
TO RECTANGLE :HEIGHT :WIDTH Echo ii [ Forwards :Top Correct 90 Forrad :WIDTH Right 90 ] Cease TO TRIANGLE :LENGTH RIGHT 45 Forrad :LENGTH * (SQRT ii) / 2 Correct 90 FORWARD :LENGTH * (SQRT 2) / 2 RIGHT 135 FORWARD :LENGTH Right 90 END TO Business firm ; draw the business firm RECTANGLE 100 100 ; draw the roof FORWARD 100 TRIANGLE 100 Dorsum 100 ; depict the door RIGHT ninety Forward threescore LEFT 180 RECTANGLE 20 xl Frontward 60 RIGHT 90 Cease HOUSE | 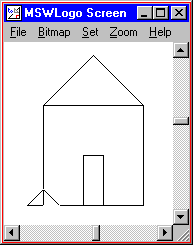 |
TO STAR :LENGTH :POINTS REPEAT :POINTS [ FORWARD :LENGTH Correct 180 - (180 / :POINTS) ] Finish STAR 200 ix | 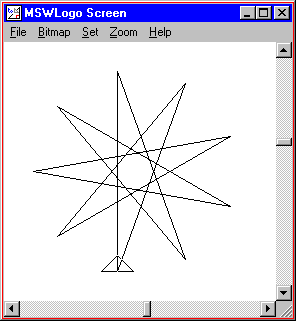 |
TO TRIANGLE :LENGTH Echo 3 [Forwards :LENGTH RIGHT 120 ] Terminate TO TRIANGLEFLOWER :LENGTH :COUNT REPEAT :COUNT [ TRIANGLE :LENGTH Correct 360 / :COUNT ] Stop TO WEB REPEAT half dozen [ TRIANGLEFLOWER REPCOUNT * 25 18 ] Stop WEB | 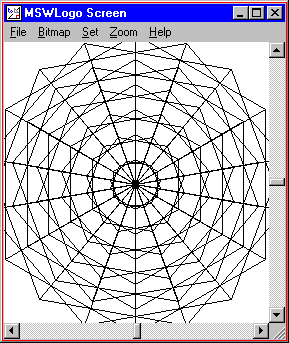 |
Challenge Questions
- How can you make shorter name for FORWARD than FD?
- How can you write a POLYGON command that draws all polygons with the same circumference?
Source: https://fmslogo.sourceforge.io/workshop/polygon.shtml